
PRINCIPIOS DEL MALABARISMO
Matemáticas y malabarismo
Teorema de Shannon
Claude Elwood Shannon dedicó los últimos años de su vida al análisis matemático del malabarismo, a Shannon se le debe la modelización y notación que se usa hoy en día para describir una rutina de malabares, como también su representación gráfica.
El modelo matemático del malabarismo se formuló antecediendo una hipótesis
1. Fijar como variables el número de manos y de objetos.
2. Suponer que al describir la figura, todas las bolas siguen la misma trayectoria y pasan todas igual tiempo en la mano. Con ello se establecen cinco parámetros:
b: Número de Bolas.
m: Número de Manos.
v: Tiempo de vuelo de cada bola.
t: Tiempo que cada mano permanece vacía.
r: Tiempo que cada bola permanece en una mano.
3. Considerar que no hay nunca dos bolas simultáneamente en la misma mano (no obstante si hay ejercicios de este tipo llamados genéricamente Multiplex) y que el ejercicio es periódico (es decir que cada configuración se repite a intervalos de tiempo determinados). Además admite que el ejercicio es simétrico y uniforme.
(tomado de http://www.malabart.com/el-teorema-de-shannon/)
A partir de todo esto, Shannon encontró una proporción fundamental que permitiría crear la notación siteswap y enunciar su teorema para el malabarismo de pelotas.
b ( r + t ) = m ( r + v )
"El tiempo que transcurre mientras la pelota está en el aire es el mismo tiempo que transcurre mientras la mano está vacía"
-Teorema de Shannon, 1980
Siteswap/Numerología del malabarismo
La modelación del malabarismo ha sido bautizada con el nombre de "Siteswap", donde se formula un patrón malabar o suceción que describe una rutina de malabares.
Siteswap trabaja por medio de números naturales, del 0 al 9.
Cada número representa una altura a la que se arroja una pelota. Para números impares, la pelota va de una mano a otra, para números pares la pelota se arroja hacia arriba y cae en la misma mano.
El número 0 representa la carencia de pelota(s) en la(s) mano(s), el número 2 significa mantener la(s) pelota(s) en la(s) mano(s) sin ser arrojada(s), todos los demás números: 1, 3, 4, 5, 6, 7, 8, 9 son las alturas de lanzamiento, que entre más alto sea el número, más alto es el lanzamiento y más tiempo ocuparía en el aire.
Creación de patrones malabar por medio de Numerología Siteswap
El uso de lo anterior mencionado se da de la siguiente manera:
Si se quiere modelizar el movimiento malabarista llamado "Cascada" (en este caso con tres pelotas)

Cascada con 3 pelotas
Las alturas de las pelotas son de 3 (nótese que las pelotas suben a la altura de los hombros).
El número de pelotas es 3.
La frecuencia de tiro es constante, es decir, no se experimentan ceros o dos.
El movimiento para la cascada en patrón malabar es
33333333... como la secuencia es periódica, el número 3 se repite constantemente, se dice que la cascada simplemente tiene un patrón de: 3
El patrón desde siteswap para simular "La lluvia" con tres pelotas es 51515151... abreviado a 51
Como son tres pelotas, se dice que está en "Siteswap 3", el patrón tiene longitud 2.
Como puede verse en la imagen en movimiento, existe una altura más arriba de la cabeza, ese es un 5 y la horizontal en la cintura es el 1.

Lluvia con 3 pelotas
La creación de estas sucesiones no es al azar, no puede ser creada una secuencia como se desee, existen reglas para su formación, si un patrón malabar cumple dos condiciones necesarios y suficientes para su validéz, entonces puede ser ejecutado.
Aquí es donde viene la parte interesante de la creación de patrones desde los criterios de divisibilidad y aritmética modular.
Las condiciones se enuncian como propiedades
Propiedad 1: Si el promedio de un patrón malabar (la suma de todos los dígitos, dividida por la cantidad de dígitos) no es un número entero, entonces la rutina no es válida. Además ese promedio es el número de bolas necesario para llevarlo a cabo.
Propiedad 2: Sea L la longitud de la rutina (N° de dígitos), N un dígito dado, y T su posición en la rutina. Luego si se toma dígito a dígito y se calcula el módulo -o resto de la división entera) de la suma N más T y L, y alguno de estos resultados se repite, entonces la rutina no es válida. En caso contrario, sí lo es.
(tomado de http://elementalidadmatematica.blogspot.com.co/p/ambiente.html)
Para más información sobre el uso de las propiedades para la formación de un patrón malabar, visite mi blog en la pestaña "artículo": http://elementalidadmatematica.blogspot.com.co/p/ambiente.html
La modelación del movimiento de las manos es algo mucho más complejo, que requiere un estudio más riguroso, por ejemplo, para modelar un movimiento como el "Factory", debe existir un modelo para el movimiento que ejecutaran las manos del malabarista.
Como puede observarse, el malabarista hace un movimiento anormal con las manos, además, las pelotas se mueven sincrónicamente por columnas. Para hacer este tipo de cosas, las manos necesitan un modelo matemático.
Al hecho de mover una pelota hacia arriba acompañada de la mano que la sujeta, se le conoce como "Fake colums".
Pero podemos analizarlo aún así desde la notación siteswap: La pelota que el malabarista sube y mueve hacia la izquierda, se toma como un 2, porque NO es arrojada, las demás pelotas son un 4. Igualmente los siteswap se vuelven más complejos, y habría que introducir conceptos más avanzados de esta notación, por ejemplo, el patrón para este movimiento es (2,4)(2,4x)(2x,4), nada que ver con lo que hemos hablado, ¿verdad?
De la misma manera, complejo o no el patrón, siempre responderá a las dos propiedades de siteswap.
Representación gráfica de un patrón malabar
Las maneras de representar lo anterior visto sobre siteswap son variadas, pero existe una común que es por medio de una recta, donde se posiciona la secuencia y por medio de "saltos" se hace la representación de lo que pasa durante la rutina. Por ejemplo, una altura de 5, representará un salto de 5 unidades.
Veamos la representación gráfica de la lluvia, recordemos que el patrón es 51:
Se observa que la primera pelota sale en 5 (recorre 5 unidades en la recta), la segunda se mueve en 1 (recorre una unidad), pero cuando esta hace ese movimiento, la que se lanzó con anterioridad aún está en 5 (va en la mitad de su trayecto), por eso, para respetar el patrón 51, la pelota que acaba de caer en la otra mano en 1, se lanza inmediatamente describiendo un 5, y así sucesivamente.
Algunos otros ejemplos de representaciones son:
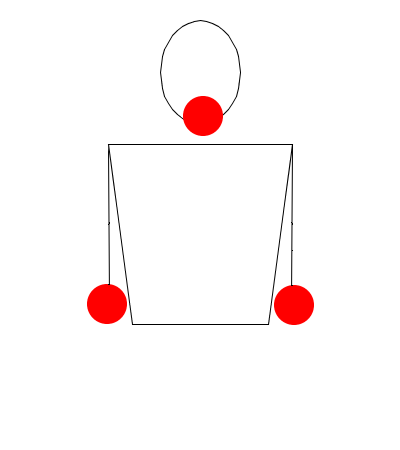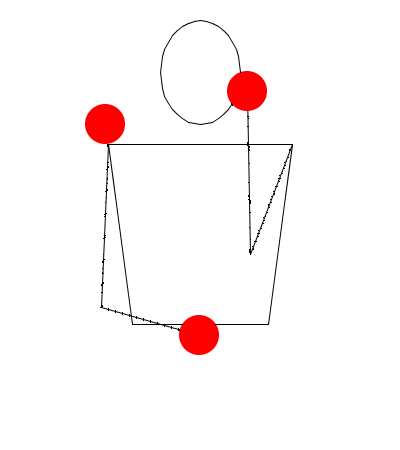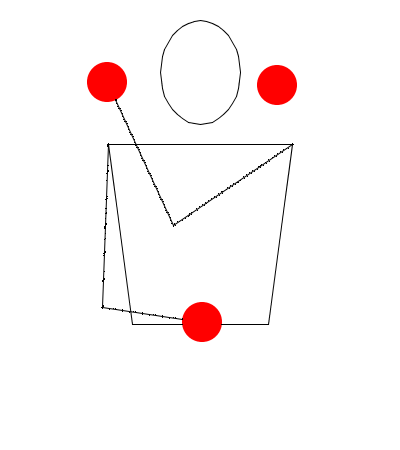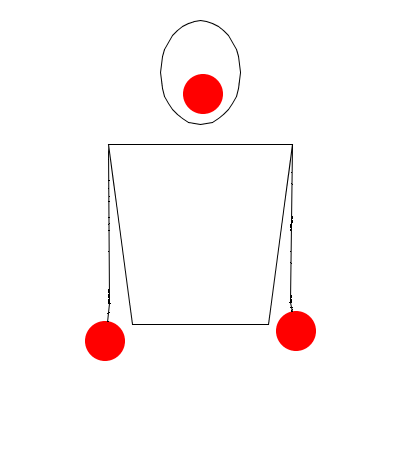
The Factory

Representación gráfica de la lluvia con tres pelotas


Representación, patrón malabar: 531
Representación, patrón malabar: 441

Representación, patrón malabar: 612
Cuando un patrón malabar es inválido (no cumple las dos propiedades de siteswap), esto es lo que pasa en la representación gráfica:

Representación, patrón malabar inválido: 243
Esto nos dice que dos pelotas caen al mismo tiempo en una sola mano, por consiguiente no puede ser representado.