ACTIVIDADES | malabar

Para las actividades que se darán a continuación, es necesario hacer estudio sobre los conceptos mensionados en la pestaña de "conceptos" del sitio.

Algunas de las siguientes actividades propuestas, requeriran el uso del applet Juggling Lab, si aún no lo tiene, puede descargarlo de la página de mi blog, haciendo click aquí. Recomiendo también complete el formulario que permite pronosticar qué tanto sabe usted sobre el tema que se trabajará a continuación, igualmente está en el blog.

ACTIVIDADES PROPUESTAS: MALABARISMO Y MATEMÁTICAS

Primer actividad: Divisibilidad entera

Como se ha visto, un patrón malabar es validado por medio de dos propiedades de divisibilidad, recordemos, una de ellas es: "si el promedio de un patrón malabar (la suma de todos los dígitos, dividida por la cantidad de dígitos) no es un número entero, entonces la rutina no es válida. Además ese promedio es el número de bolas necesario para llevarlo a cabo"

Haciendo uso de esta propiedad, encuentre la validez de las siguientes rutinas

5342
435
352
441
4264
3161
531
432
64723
6451

Habiendo encontrado si la primera propiedad se cumple para las rutinas, usando el applet Juggling Lab, simule cada una.

Responda lo siguiente:

¿Porqué el applet no simula todas las rutinas que validaron la primera propiedad?

¿Qué nos dice el promedio encontrado en cada rutina válida?

Segunda actividad: Módulo de una división entera

Recordemos la segunda propiedad de una patrón malabar: "sea L la longitud de la rutina (N° de dígitos), N un dígito dado, y T su posición en la rutina. Luego si se toma dígito a dígito y se calcula el módulo (o resto de la división entera) de la suma N más T y L, y alguno de estos resultados se repite, entonces la rutina no es válida. En caso contrario, sí lo es".

Para las rutinas enunciadas en la anterior actividad, encuentre en el siguiente orden

L para cada rutina
Asigne un valor N para cada dígito
Asigne un valor T para cada dígito

Habiendo aclarado esto, haga uso de la aritmética modular, y encuentre:

(N+T) mod L

Responda:

¿Se repiten los módulos para cada dígito, en cuales rutinas?

¿Qué rutinas cumplen la primera propiedad y la segunda?

Haga una simulación en Juggling Lab de los patrones que satisfacen ambas propiedades.

Tercera actividad: Modelación de una rutina (Siteswap - sucesiones)

Primera parte

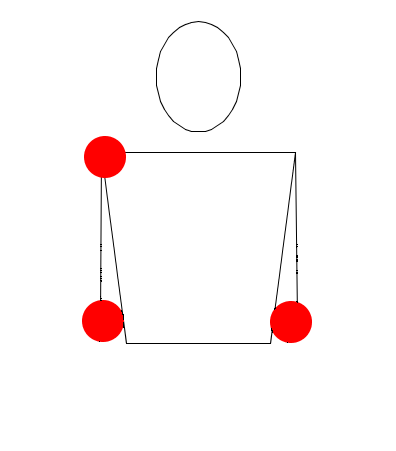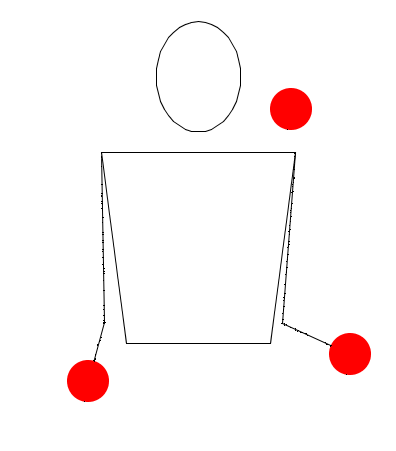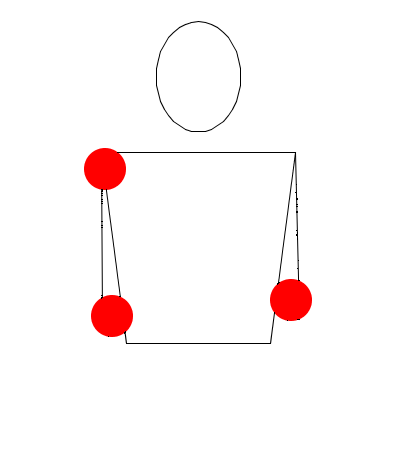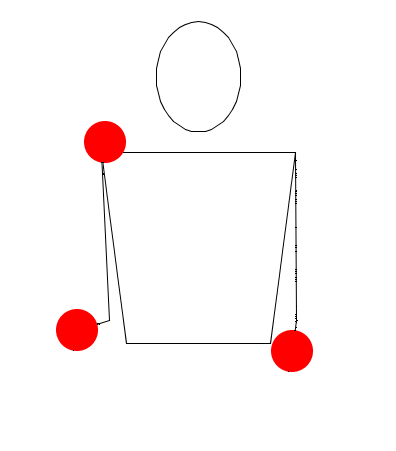
Observe las siguientes rutinas de malabares simuladas en Juggling Lab:

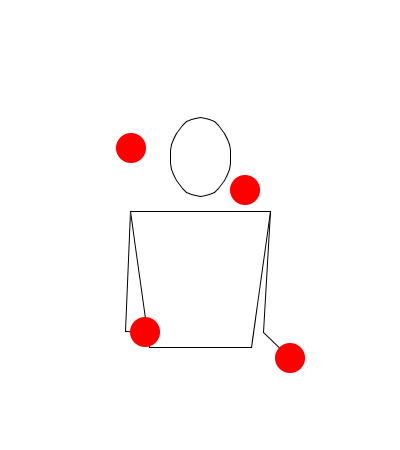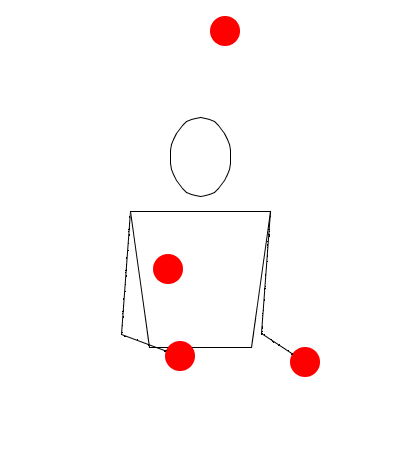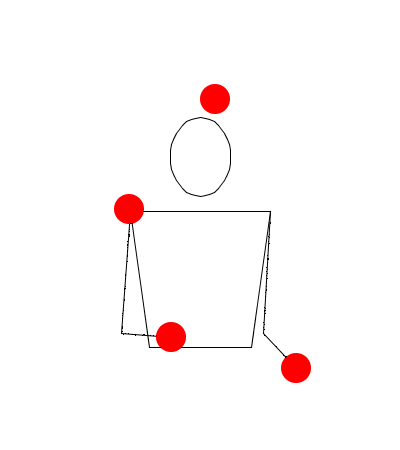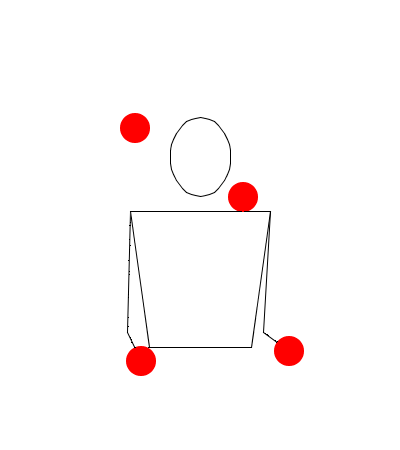
Rutina uno

Rutina dos

Rutina tres

Rutina cuatro

Rutina cinco

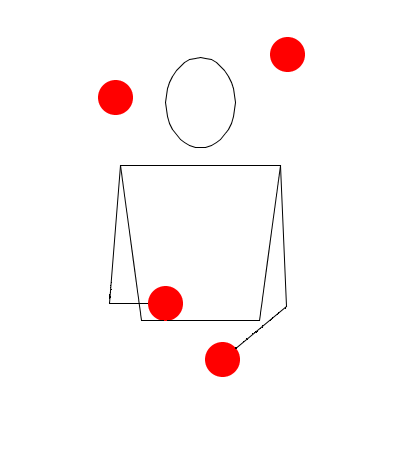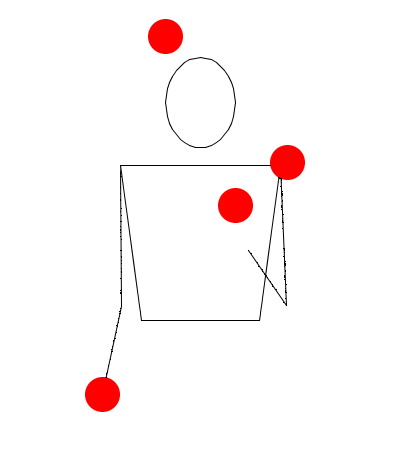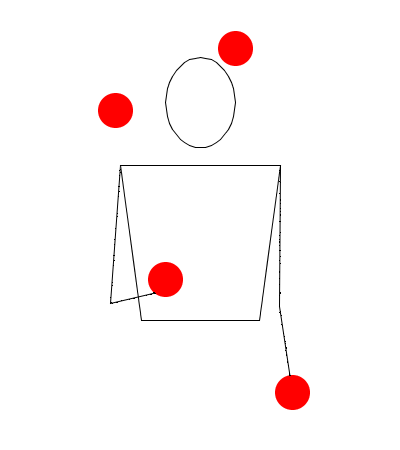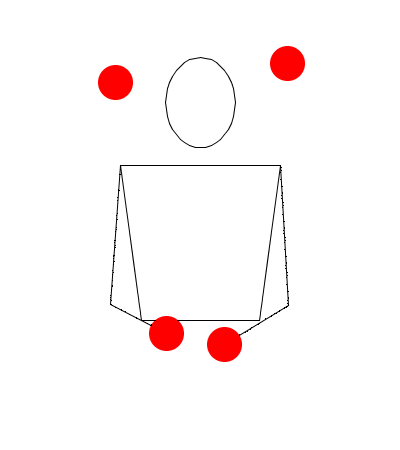
Rutina seis

Observe muy bien las rutinas, recuerde que no estamos trabajando sobre hands movement modelation (modelación del movimiento las manos), así que no lo tenga en cuenta, solamente exprese en sucesiones (Numerología/Siteswap) cada una de las seis rutinas, deduciendo las alturas de las pelotas, y teniendo en cuenta las propiedades de validez, principalmente la primera.

Segunda parte

Observando las siguientes simulaciones, responda: ¿Corresponde la sucesión dada al movimiento descrito con Juggling Lab? (Responda: falso o verdadero)

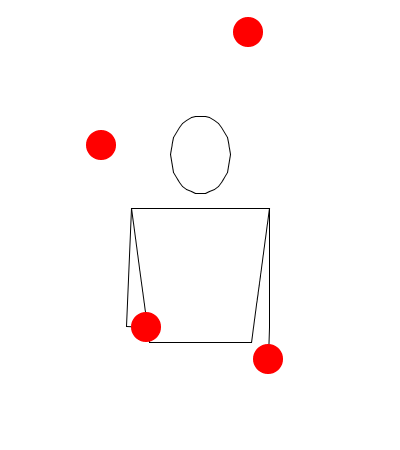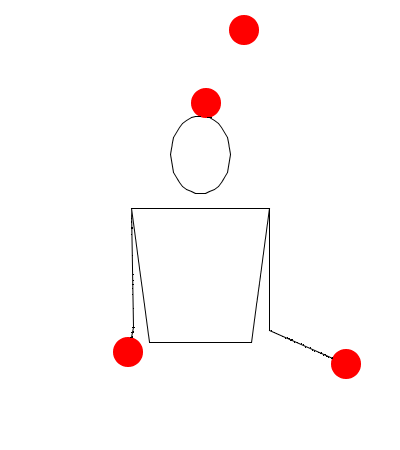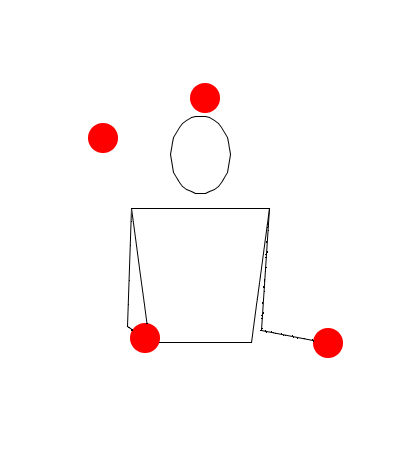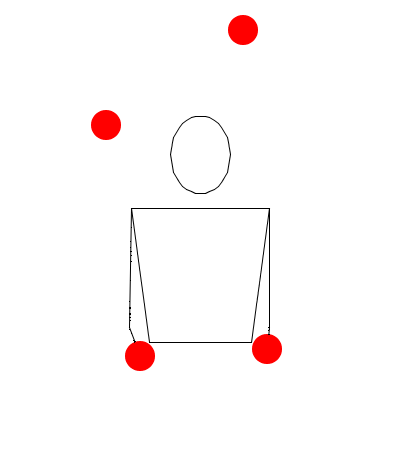
552

5155

6

51

81

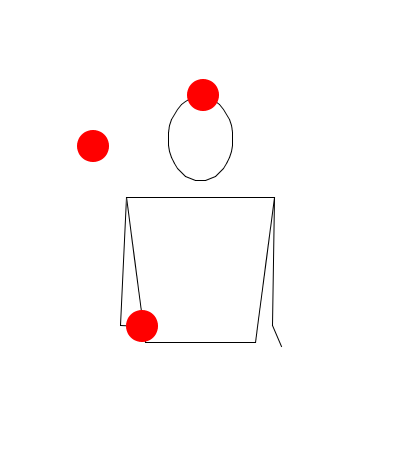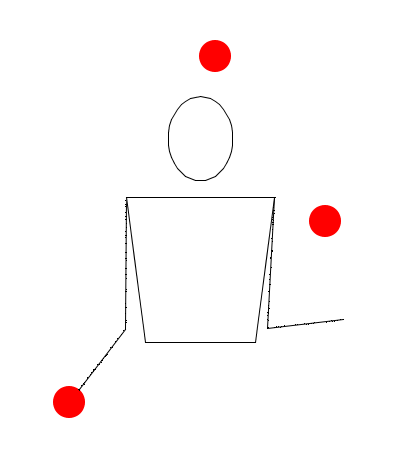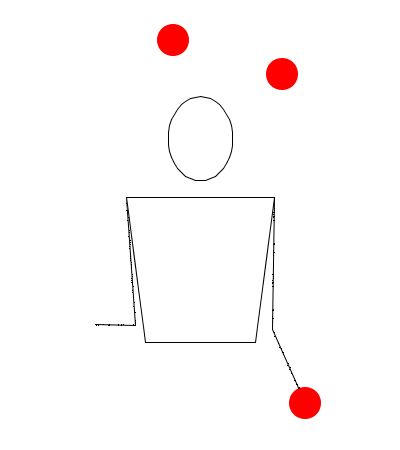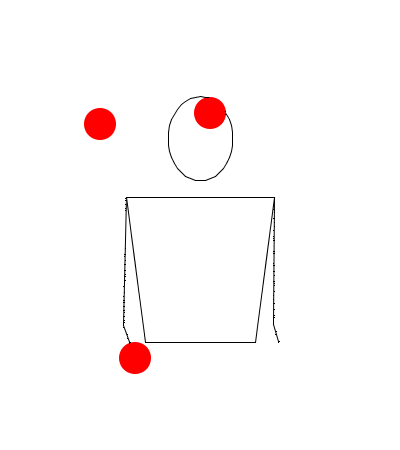
3404

De ser una rutina con un patrón malabar falso, proponga el patrón que en verdad la modeliza, teniendo en cuenta las propiedades y lo observado en la simulación.

Tercera parte

Recuerde los conceptos de la representación gráfica de un patrón malabar, trabajados en la pestaña de "conceptos".

Represente las siguientes sucesiones (patrones malabar) con el método gráfico, y desde este, responda para cada sucesión: ¿porqué es válida o inválida?

333
71717171
547
8364
24323
531
441
4019
55001
5550

Adicional a eso, responda la siguiente pregunta:

¿Cuándo se dice que dos pelotas caen al mismo tiempo en una mano, por medio de la representación gráfica?

Cuarta parte

Esta es una actividad variada

Analice las siguientes sucesiones:

¿Qué sucesión describe esta representación de la rutina?

Ciertamente esta rutina empieza en 33333, pero desde el sexto lanzamiento, existe un cambio. ¿Qué sucesión representa esta nueva rutina?

¿Es valida la sucesión mostrada en la representación gráfica para ese patrón malabar?

Observe la siguiente simulación de Juggling Lab:

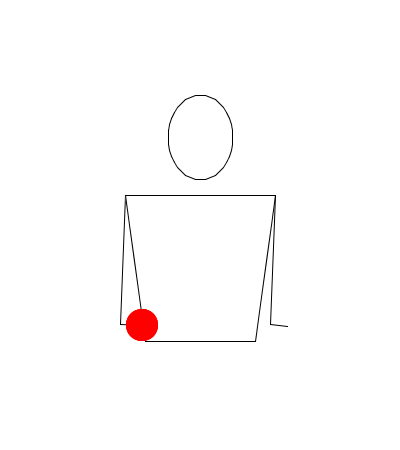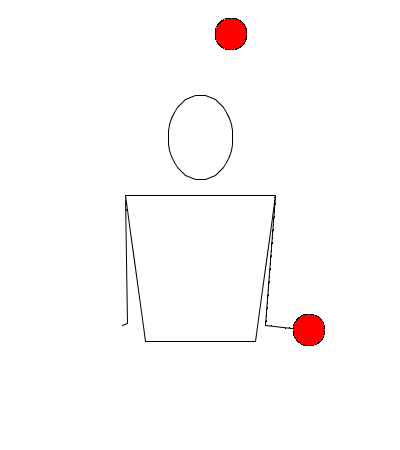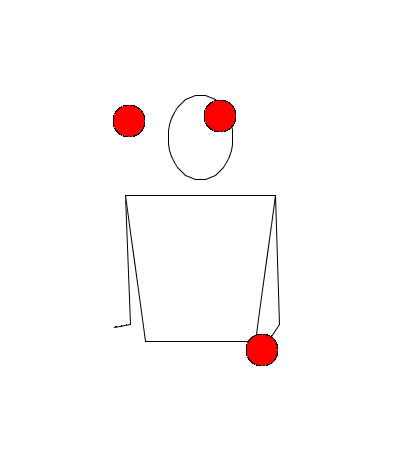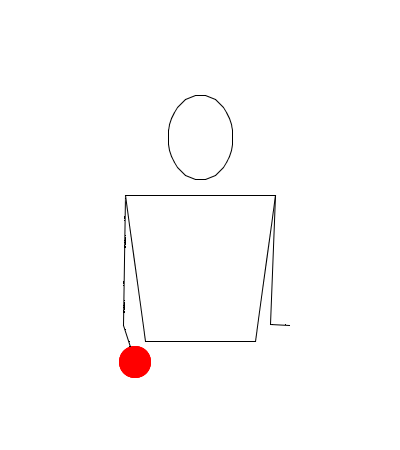
¿Por qué el método de representación gráfica invalidaría esta rutina?

¿Sabias qué...

"Multiplex" es el denominado a la modelación de pelotas que caen en instantes iguales, en manos iguales. La modelación del patrón malabar, a medida que evolucionaba desde 1980, logró diseñarse un modelo que representara la caida de dos pelotas en una mano, se representa con corchetes en el patrón ([35]1231, por ejemplo).

Ejemplo de Multiplexación

Quinta parte

Inicie el software Juggling Lab, diríjase a la pestaña "Generador", allí usted podrá generar todos los patrones posibles con determinado número de pelotas, determinada longitud del patrón malabar, determinada altura máxima, con opción de multiplex, sincronía, entre otras.

Lo que usted debe hacer, es escoger opciones como lo desee (Sin multiplexación y en ritmo asincrónico), luego generar todos los patrones posibles, por ejemplo, para 4 pelotas en tiro máximo 5 y periodisidad 4, Juggling Lab arroja una lista como esta:

Ahora, habiendo escogido su lista de patrones, elija 4 patrones malabar de su preferencia, y haga una representación gráfica de ellos.

Lista de patrones posibles

Pelotas: 4

Tiro máximo: 5

Periodo: 4

________________________________

ACTIVIDADES PROPUESTAS: MALABARISMO Y FÍSICA

En la pestaña de "conceptos/física", se explicó sobre las relaciones existentes entre la cinemática unidimensional y los movimientos en columns o columnas, de igual manera la cinemática bidimensional, los cruces y demás movimientos parabólicos del movimiento de las pelotas en una rutina de malabares.

Con base a lo aprendido, y sus conocimientos sobre cinemática, realice las siguientes actividades

Primera actividad: Movimiento unidimencional (vertical)

Situaciones problema

1. Un malabarista desea saber la velocidad necesaria para la ejecución del lanzamiento de las pelotas en "pistones" con 4 pelotas (444...), sabiendo que la altura promedio para un 4 es h = 90 cm.

Pistones con 4 pelotas

Adicional a eso, halle el tiempo que cada pelota permanece en el aire.

2. Francis Brunn (1922 - 2004) fue un gran malabarista reconocido por su especialidad de ejecutar malabares con la cabeza. Cuando Brunn hacía columnas con una pelota, esta alcanzaba una altura de h = 3 mts aproximadamente (era una pelota especial de goma, que rebotaba facilmente)

¿Con qué velocidad llegará la pelota a la cabeza de Brunn en el descenso?

3. "The Box" es un reconocido patrón malabar, para su representación se usa la notación de synchronized siteswaps o siteswap sincrónicos (4,2x)(2x,4)

Suponga que cuando se lanza la pelota que se mueve en columna en la mano derecha, asciende con una velocidad inicial de 3 m/s. ¿Qué tiempo transcurre para el lanzamiento de la pelota de la mano izquierda, desde que se lanza la de la mano derecha?
Recuerde que es un movimiento sincrónico.

Francis Brunn

The Box

Dato curioso: esta es la representación de

(4,2x)(2x,4) en un diagrama

Representación de "The Box" en diagrama

Segunda actividad: Movimiento bidimensional (parabólico)

Situaciones problema

1. Supóngase que la separación de las manos de un malabarista al momento de arrojar una pelota es siempre x = 70 cm.

Un 5 tiene en promedio h = 1,2 mts.

¿Con qué velocidad y ángulo de inclinación deben ser arrojadas las pelotas en cascada con 5 pelotas?

2. Cuando se hace fountain o fuente con 4 pelotas, el malabarista mantiene dos pelotas en una mano, y dos en la otra, la parábola que describe cada pelota es igual, puesto que el patrón malabar es 4 (444...). Si se quiere que una de las pelotas describa un 6, habría que modificar el patrón, y en él aparecerían ceros (0) o dos (2), con el fin de compensar la altura agregada. ¿A que altura habría que arrojar ese 6, sabiendo que el 0 o 2, debe durar aproximadamente 1,4 segundos?

Tenga en cuenta que la altura promedio para un 4 es de 90 cm.

El ángulo de inclinación para mantener la pelota en una mano es 80°

La distancia horizontal que recorre la pelota es de 40 cm

Tercera actividad: Dinámica malabarista

1. Un malabarista en su rutina de malabares, lanza una pelota que hace fallar el truco, el malabarista excedió la fuerza necesaria para que la pelota describiese el movimiento que debiese hacer realizado. La pelota tiene una masa m = 400 g, la aceleración necesaria para el lanzamiento de la pelota es de 170 cm/s^2. ¿Qué fuerza debió haber aplicado el malabarista para evitar perder el control de la pelota? exprese el resultado en [dinas]

2. Además del malabarismo tradicional Juggling existe el malabarismo de contacto Contact Juggling, el cual consiste en rodar la pelota por diferentes sectores del cuerpo

Observe la imagen, si la bola de cristal tiene una masa de 650 gr, ¿Qué fuerza tiene que ejercer la malabarista con el dedo pulgar, para que el sistema mano-pelota esté en equilibrio?

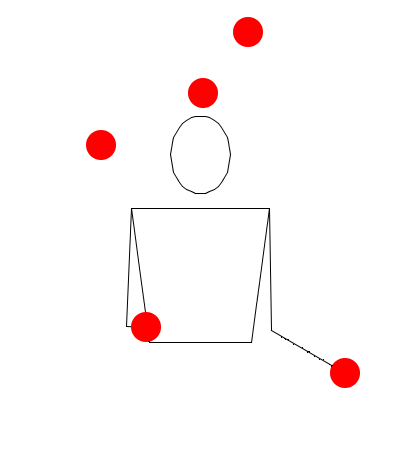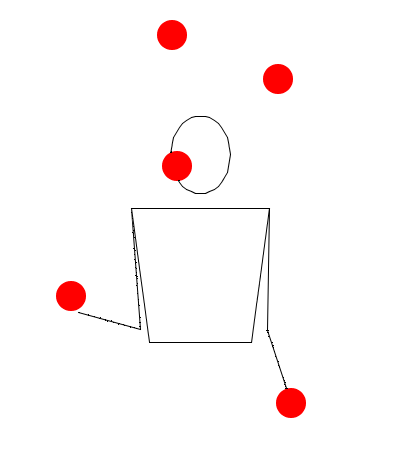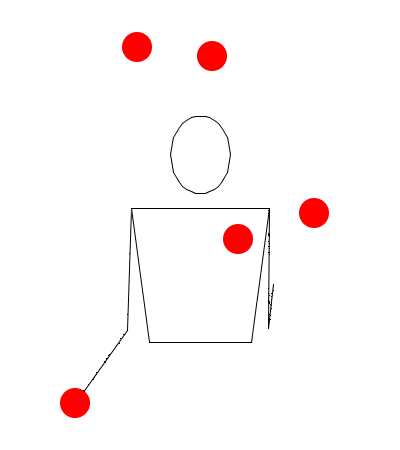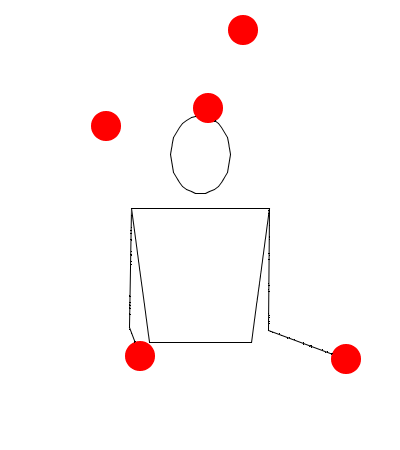
Cascada con 5 pelotas

Fuente con 4 pelotas

Contact Juggling